Technique: Cheap speed

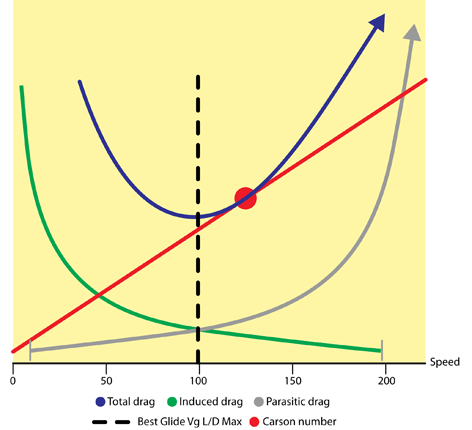
Sometimes pilots want to maximize speed and don’t care how much fuel they burn (think Reno racers). Other flights require slowing down for max range (think P–38s over the Pacific).

Between these extremes, however, there’s a sweet spot where pilots can take advantage of a rare aerodynamic bargain: significantly higher speed for a relatively small rise in fuel consumption. And even though it’s not marked on any airspeed indicator, the optimum place for speed over fuel consumption (known as the “Carson number” for B.H. Carson, the aerodynamicist who identified it) is surprisingly easy to find.

“Accepting that excess fuel is to be traded off for airspeed during normal operations, there is a method of operation which represents the ‘least wasteful way of wasting fuel,’” Carson wrote in a pioneering 1980 study.

First, some background. We all learn in ground school about that singular place on the total drag curve where the amount of lift over drag is the highest (L/D max). That number is reflected in aircraft pilot’s operating handbook as the best-glide speed (V _G). A typical piston airplane’s maximum-range speed is about 10 percent above L/D max (or 25 percent for turbojets), and that’s where pilots can get the most miles per gallon out of their airframes.

Sadly, however, L/D max and max range speeds are usually very small numbers, and few pilots have the patience or inclination to plod along there for hours to get to distant destinations. We’re willing to buy a lot more avgas for the privilege of getting where we want to go much faster. Intellectually, we know there’s a tradeoff between speed and efficiency, but we don’t know exactly how to balance the two seemingly mutually exclusive goals.

In his innovative study of aircraft efficiency, however, Carson identified and quantified the costs and benefits. And he determined that a 32-percent increase in airspeed over L/D max is available for a mere 16 percent in added fuel consumption (excluding variables such as wind and propeller efficiency).

Add a gain in true airspeed by flying at relatively high altitude (true airspeed increases roughly 20 percent over indicated airspeed at 10,000 feet), and pilots can increase the speed they travel an impressive 52 percent for that same 16-percent rise in fuel consumption. That’s some very cheap speed! Beyond the Carson number, however, the aerodynamic bargain turns into a fleecing as the price of each additional knot quickly becomes exorbitant.

So how do we find this optimum place at which we get the biggest increase in airspeed for the smallest fuel penalty? Simply multiply your airplane’s best-glide speed by 1.316—or add 32 percent—and that’s the Carson number.

The real world

So how can pilots apply this theory in practice?

On a recent flight in a 1972 Bonanza A36 (with a Continental IO-550 engine and 74 gallons of usable fuel), I planned an 800-nm trip from Cloquet, Minnesota, to Frederick, Maryland, with the Carson number in mind.

The Bonanza POH sets the V _G at 110 knots. So 110 knots (V _G) times 1.316 equals 144.76 KIAS. Rounding that number up, 145 KIAS was our target airspeed.

With nose-hoses attached to an oxygen bottle, AOPA photographer Chris Rose and I took off and set a course for Frederick (via Martinsburg, West Virginia), climbing at 120 KIAS and leveling off at 11,000 feet. Airspeed increased to 148 KIAS on this warm summer morning, and pulling the mixture to a lean-of-peak setting at 2,500 rpm slowed the Bonanza to 142 KIAS (174 KTAS)—just three knots shy of the Carson number.

In no-wind conditions, this would have got us home at an optimum speed relative to fuel flow. But this being the real world, it wasn’t that easy—and there were other factors to consider. A 15-knot headwind reduced our groundspeed, and the Bonanza’s JP Instruments fuel computer let us know we’d have legal, but personally insufficient, reserves of less than one hour at our destination unless something changed.

With apologies to Professor Carson, it was time to trade some of that speed for greater range.

At 13,000 feet the wind direction improved, and we were rewarded with an increase in groundspeed. With intermittent IMC and an OAT near freezing at that altitude, however, we continued the climb to 15,000 to stay clear of clouds. There, our indicated airspeed of 126 knots was just five knots above max range (110 knots V _G plus 10 percent equals 121 KIAS), fuel consumption dropped to 9.8 gph (from 12.4 gph), and true airspeed fell to 164 knots.

The reduced fuel consumption and less adverse winds allowed us to skip an intermediate fuel stop in the sweltering Ohio Valley and continue nonstop to our destination on the even-more-sweltering East Coast.

After five hours aloft (at an average groundspeed 160 knots) we touched down at our home airport with 15 gallons of fuel remaining (or 59 gallons consumed out of 74 usable). Five hours is a long time to sit still, and many pilots refuse to fly long legs for this reason alone. But the nonstop trip avoided an additional takeoff and landing, a hot start, and a full-power climb back to altitude that would have pushed the engine’s cylinder head temperatures near the red line. Better to keep the engine happily loafing along at 52 percent power in the smooth, cool air above.

We certainly didn’t set any speed records, but the combination of high altitude, a lean-of-peak power setting, and an efficient cruise speed show that even an airplane some pilots consider range limited can still cover long distances.

E-mail the author at [email protected].