A new look at maneuvering speed
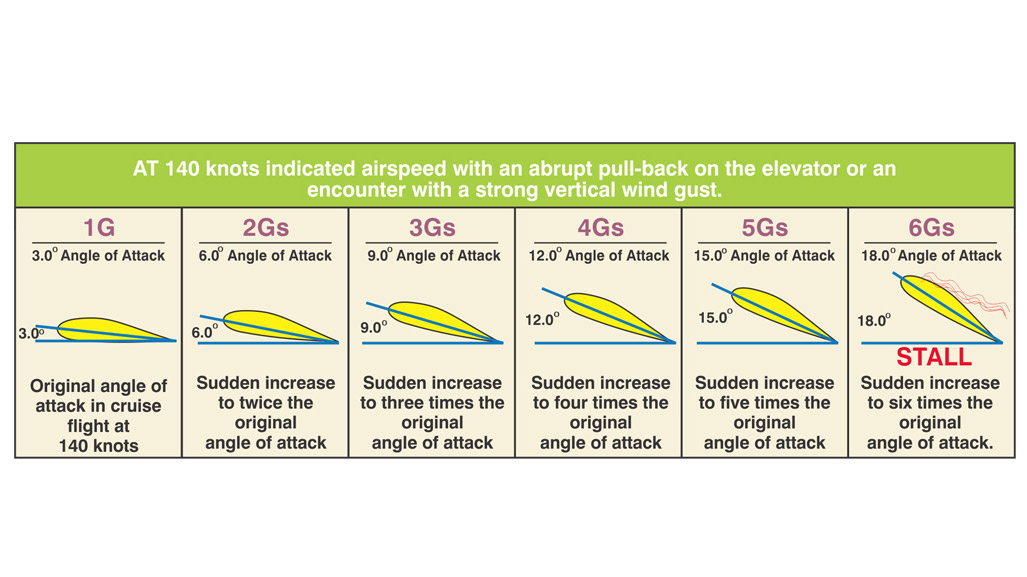
Illustration from Rod Machado’s Private Pilot Handbook.
Even though the wings are subject to lots of stress, you needn’t worry about them breaking as long as you do one thing. Simply keep the airplane at or below its designed maneuvering speed in turbulence. Here’s how this works.
The design maneuvering speed (VA) is the speed at which the airplane will stall before exceeding its design limit-load factor in turbulent conditions or when the flight controls are suddenly and fully deflected in flight. Under these conditions the airframe experiences an increase in “G-force” or “load factor.”
The limit-load factor of U.S. certificated airplanes is based on the maximum amount of G-force the airframe can withstand before becoming damaged. Airplanes stressed up to but not beyond their limit-load factor should experience no structural damage. (This assumes the airplane is like new and not previously over-stressed.)
For the purposes of airplane certification, airplanes are certified in one of three categories: normal, utility, aerobatic. Each category has stress limits of: +3.8Gs and -1.52Gs for normal category airplanes; +4.4Gs and -1.76Gs for the utility category airplane; +6Gs and-3Gs for the aerobatic category airplane. Let’s examine how maneuvering speed prevents us from exceeding these limits.
Standing anywhere on planet Earth, you’ll experience “one” times the force of gravity, or 1 G. It’s gravity that pulls you toward Earth’s center, providing the feeling of weight. On the surface, gravity exerts a constant 1-G pull. In an airplane, however, you and the airplane can feel like you weigh more than your actual weight. This occurs when the airplane turns or the angle of attack suddenly increases (as it does in turbulence). This increase in apparent weight is called an increase in “G-force” or “load factor.”
Let’s suppose our airplane is cruising in straight and level flight at a constant airspeed. In this condition, lift is equal to weight and we experience a G-force of 1. We can represent G-force by the formula: Lift/Weight = G-force.

Illustration from Rod Machado’s Private Pilot Handbook.
In straight and level, unaccelerated flight the lift developed by the wings is equal to the airplane’s weight. Thus, the G-force is 1 G.
If the angle of attack suddenly increased (by pulling back on the elevator or encountering a vertical gust of wind for example), the wings would produce an instantaneous increase in lift. The airplane accelerates upward and you’re forced downward in your seat. In other words, there is more upward pull by lift compared to the downward pull by weight. The G-force increases proportionally to the sudden increase in lift. Instantaneously doubling, tripling or quadrupling the lift, doubles, triples, or quadruples the G-force.
A direct (or nearly so), one-to-one relationship exists between lift and angle of attack. For instance, at a constant airspeed, in a 1-G condition, a sudden doubling of the angle of attack doubles the wing’s lift and doubles the G-force. Tripling or quadrupling the angle of attack triples or quadruples the G-force.
For instance, assume the airplane is flying at a fast cruise speed of 140 knots as shown in Figure 1. The airplane and its contents experience 1 G at an angle of attack of 3 degrees for level flight. Suppose a sudden gust increases the angle of attack by an additional 3 degrees. The wing’s original angle of attack has now doubled to 6 degrees (3+3=6). Consequently, lift suddenly doubles, producing 2 Gs. A sudden increase in angle of attack to 9 degrees triples the lift and the G-force. An increase to 12, 15 and 18 degrees increases the lift and G-force to four, five and six times its original value.
Since the wing stalls (and lift production decreases) at approximately 18 degrees angle of attack, any further increase in angle of attack beyond six times the original value of 3 degrees won’t increase the G-force. Therefore, at 140 knots this airplane is capable of experiencing 6 Gs before the wings stall. If the airplane in this example had a limit load factor of 4 Gs, the structure might experience some damage at this speed in strong turbulence. (I chose 4 Gs instead of the actual limit loads of +3.8, +4.4 or +6 Gs for this example to simplify the math.)
If we slow our airplane down to 110 knots (Figure 2), then a 4.5 degree angle of attack is necessary for a 1 G, level-flight condition. If, at 110 knots, we suddenly double the original angle of attack to 9 degrees, the lift doubles. We now feel 2 Gs. A sudden tripling of the original angle of attack to 13.5 degrees triples the lift and we experience 3 Gs. And finally, quadrupling the original angle of attack to 18 degrees produces four times as much lift. Therefore, we experience 4 Gs. It’s not possible to pull more than 4 Gs in this example since the airplane will stall at 18 degrees. Consequently, 110 knots is the maneuvering speed for our airplane having a limit-load factor of 4 Gs. At 110 knots, the airplane will stall before it exceeds this limit load factor in turbulent air or with full deflection of the flight controls. (Personally, in turbulence, I prefer to fly 10 to 15 knots below VA to prevent a gust from temporarily raising my indicated airspeed above VA.)
Whether a specific gust doubles, triples, or quadruples the angle of attack depends on the angle of attack of the airplane in its 1 G condition. As is clearly evident from these examples, it’s easier for a gust to double, triple, or quadruple the angle of attack over its starting value when the airplane is flying faster (because it’s at a lower angle of attack to begin with). Consequently, it’s easier to experience more Gs for a given amount of turbulence at higher airspeeds.
Weight change and VA
Maneuvering speed is based on the airplane being at gross weight. What happens when the airplane’s weight decreases? The answer is: the maneuvering speed decreases. Let me explain.
Airplanes flown at weights below their gross weight require less lift for straight and level flight. Less lift means the airplane can be flown at a smaller angle of attack. In other words, an airplane at 2,500 pounds may require a 4.5 degree angle of attack at 110 knots to remain in level flight. Decreasing the weight to 1,800 pounds may require only a 3 degree angle of attack to remain in level flight at this speed. Does this angle of attack sound familiar to you?
With a speed of 110 knots, at this lower weight, a sudden and very strong gust could increase the angle of attack from 3 to 18 degrees. From our previous example, this produces six times the original lift for a force of 6 Gs. This is way beyond the limit of a normal category airplane. At lighter weights, what can we do to keep from exceeding our example limit of 4 Gs when in turbulence?
The answer is to slow the airplane down. At a slower speed (95 knots for example) a larger angle of attack (let’s say 4.5 degrees) is necessary for level cruise flight at this lower weight.
At this speed, we can increase the angle of attack four times before the airplane stalls. Ninety-five knots becomes our new maneuvering speed if we want to limit ourselves to 4 Gs. Thus, decreasing weight requires a decrease in the airplane’s maneuvering speed.
Most of the newer pilot’s operating handbooks publish two or three different maneuvering speeds for variable weight conditions. If yours doesn’t, try doing the following to compute a new one. For every 2-percent reduction in weight, reduce the maximum-weight maneuvering speed by 1 percent. In other words, if the gross weight decreases by 20 percent, reduce the max-gross weight maneuvering speed by 10 percent. This is simple math. (Besides, don’t feel too bad if you are confused about math. For many years, I thought the logarithms was a singing group at MIT.)
A few final words. If you encounter turbulence in flight, fly a level flight attitude. Attempting to hold altitude at the expense of maintaining the proper airspeed might overstress the airplane. For those engineers reading this, I assume that the zero-lift angle of attack is zero degrees. A linear-lift curve is also assumed with a lift coefficient that increases 0.1 for each degree angle of attack increase (this is close enough to the real world for our purposes).



